Các bài toán saud đây đều cho trong hệ toạ độ Oxyz.
1. Cho bốn điểm A(1 ; 0 ; 0), B(0 ; 1 ; 0), C(0 ; 0 ‘ 1), D(-2 ; 1 ; -1).
a) Chứng minh A, B, C, D là bốn đỉnh của một tứ diện
b) Tìm góc giữa hai đường thẳng AB và CD.
c) Tính độ dài đường cao của hình chóp A.BCD.
2. Cho mặt cầu (S) có đường kính là AB biết rằng A(6 ; 2 ; -5), B(-4 ; 0 ; 7).
a) Tìm toạ độ tâm I và bán kính r của mặt cầu (S).
b) Lập phương trình của mặt cầu (S).
c) Lập phương trình của mặt phẳng (α) tiếp xúc vwois mặt cầu (S) tại điểm A.
3. Cho bốn điểm A(-2 ; 6 ; 3), B(1 ; 0 ; 6), C(0 ; 2 ; -1), D(1 ; 4 ; 0).
a) Viết phương trình mặt phẳng (BCD). Suy ra ABCD là một tứ diện.
b) Tính chiều cao AH của tứ diện ABCD.
c) Viết phương trình mặt phẳng (α) chứa AB và song song với CD.
4. Lập phương trình tham số của đường thẳng:
a) Đi qua hai điểm A(1 ; 0 ; -3), B(3 ; -1 ; 0).
b) Đi qua điểm M(2 ; 3 ; -5) và song song với đường thẳng Δ có phương trình
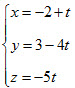
5. Cho mặt cầu (S) có phương trình: (x - 3)2 + (y + 2)2 + (z - 1)2 = 100 và mặt phẳng (α) có phương trình 2x – 2y – z + 9 = 0. Mặt phẳng (α) cắt mặt cầu (S) theo một đường tròn (C).
Hãy xác định toạ độ tâm và tính bán kính của đường tròn (C).
6. Cho mặt phẳng (α) có phương trình 3x + 5y – z – 2 = 0 và đường thẳng d có phương trình
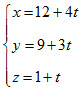
a) Tìm giao điểm M của đường thẳng d và mặt phẳng (α).
b) Viết phương trình mặt phẳng (β) chứa điểm M và vuông góc với đường thẳng d.
7. Cho điểm A(-1 ; 2 ; -3), vecto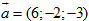 
và đường thẳng d có phương trình :
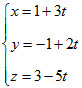
a) Viết phương trình mặt phẳng (α) chứa điểm A và vuông góc với giá của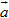 
.
b) Tìm giao điểm của d và (α).
c) Viết phương trình đường thẳng Δ đi qua điểm A, vuông góc với giá của 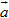và cắt đường thẳng d.
8. Viết phương trình mặt phẳng (α) tiếp xúc với mặt cầu
(S) : x2 + y2 + z2 - 10x + 2y + 26z + 170 = 0
Và song song với hai đường thẳng
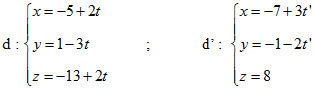
9. Tìm toạ độ điểm H là hình chiếu vuông góc của điểm M(1 ; -1 ; 2) trên mặt phẳng (α) : 2x – y + 2z + 11 = 0.
10. Cho điểm M(2 ; 1 ; 0) và mặt phẳng (α) : x + 3y – z – 27 = 0. Tìm toạ độ điểm M’ đối xứng với M qua (α).
11. Viết phương trình đường thẳng vuông góc với mặt phẳng toạ độ (Oxz) và cắt hai đường thẳng
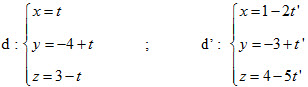
12. Tìm toạ độ điểm A’ đối xứng với điểm A(1 ; - 2 ; -5) qua đường thẳng Δ có phương trình
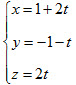
CÂU HỎI TRẮC NGHIỆM CHƯƠNG III Trong không gian Oxyz cho ba vecto
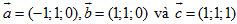
Sử dụng giả thiết này để trả lời các câu hỏi 1, 2 và 3 sau đây.
1. Trong các mệnh đề sau, mệnh đề nào sai?
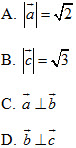
2. Trong các mệnh đề sau, mệnh đề nào đúng?
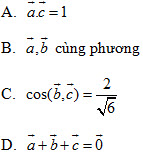
3. Cho hình bình hành OADB có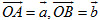 
(O là gốc toạ độ). Toạ độ của tâm hình bình hành OADB là:
A. (0 ; 1 ; 0)
B. (1 ; 0 ; 0)
C. (1 ; 0 ; 1)
D. (1 ; 1 ; 0)
4. Trong các mệnh đề sau đây, mệnh đề nào sai?
A. Bốn điểm A, B, C, D tạo thành một tứ diện
B. Tam giác ABCD là tam giác đều
C. AB ⊥ CD
D. Tam giác BCD là tam giác vuông
5. Gọi M, N lần lượt là trung điểm của AB và CD. Tìm toạ độ điểm G là trung điểm của MN là :
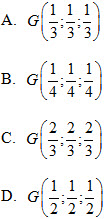
6. Mặt cầu ngoại tiếp tứ diện ABCD có bán kính là:
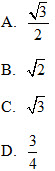
7. Cho mặt phẳng (α) đi qua điểm M(0 ; 0 ; -1) và song song với giá của hai vecto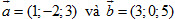 
.
Phương trình của mặt phẳng (α) là:
A. 5x – 2y – 3z – 21 = 0
B. -5x + 2y + 3z + 3 = 0
C. 10x – 4y – 6z + 21 = 0
D. 5x – 2y – 3z + 21 = 0
8. Cho ba điểm A(0 ; 2 ; 1), B(3 ; 0 ; 1), C(1 ; 0 ; 0). Phương trình mặt phẳng (ABC) là:
A. 2x – 3y – 4z + 2 = 0
B. 2x + 3y – 4z – 2 = 0
C. 4x + 6y – 8z + 2 = 0
D. 2x – 3y – 4z + 1 = 0
9. Gọi (α) là mặt phẳng cắt ba trục toạ độ tại ba điểm M(8 ; 0 ; 0), N(0 ; -2 ; 0), P(0 ; 0 ; 4). Phương trình của (α) là:
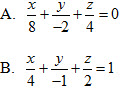
C. 4x + 6y – 8z + 2 = 0
D. x – 4y + 2z – 8 = 0
10. Cho ba mặt phẳng (α) : x + y + 2z + 1 = 0
(β) : x + y – z + 2 = 0
(γ) : x – y + 5 = 0
Trong các mệnh đề sau đây, mệnh đề nào sai?
A. (α) ⊥ (β)
B. (γ) ⊥ (β)
C. (α) // (γ)
D. (α) ⊥ (γ)
11. Cho đường thẳng Δ đi qua điểm M(2 ; 0 ; -1) và có vecto chỉ phương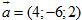 
. Phương trình tham số của đường thẳng Δ là:
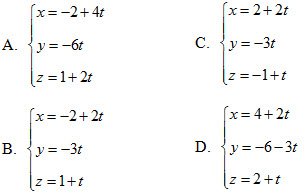
12. Cho d là đường thẳng đi qua điểm A(1 ; 2 ; 3) và vuông góc với mặt phẳng (α) : 4x + 3y – 7z + 1 = 0.
Phương trình tham số của d là :
13. Cho hai đường thẳng
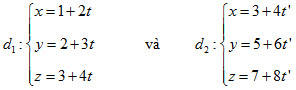
Trong các mệnh đề sau, mệnh đề nào đúng?
A. d1 ⊥ d2
B. d1 // d2
C. d1 ≡ d2
D. d1 và d2 chéo nhau
14. Cho mặt phẳng (α) : 2x + y + 3z + 1 = 0 và đường thẳng d có phương trình tham số :
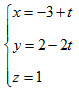
Trong các mệnh đề sau, mệnh đề nào đúng?
A. d ⊥ (α)
B. d cắt (α)
C. d // (α)
D. d ⊂ (α)
15. Cho (S) là mặt cầu tâm I(2 ; 1 ; -1) và tiếp xúc với mặt phẳng (α) có phương trình : 2x – 2y – z + 3 = 0.
Bán kính của (S) là:
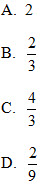
BÀI ĐỌC THÊM
CHÙM MẶT PHẲNG
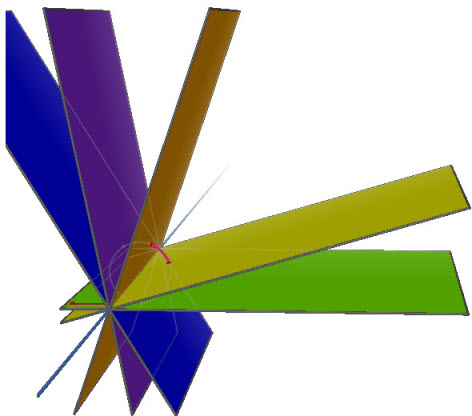
Hình 3.18
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12cb_Ch3_h3.18.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
Trong không gian cho hai mặt phẳng (α) và (β) cắt nhau theo giao tuyến Δ. Tập hợp các mặt phẳng (γ) chứa đường thẳng Δ nói trên được gọi là chùm mặt phẳng xác định bởi (α) và (β) và kí hiệu là ((α), (β)).
Nếu (α) và (β) lần lượt có phương trình (α) : A1x + B1y + C1z + D1 = 0 (β) : A2x + B2y + C2z + D2 = 0 thì người ta chứng minh được phương trình của chùm mặt phẳng ((α), (β)) có dạng:
m(A1x + B1y + C1z + D) + n(A2x + B2y + C2z + D2) = 0 (1)
với m2 + n2 ≠ 0.
Phương trình (1) có thể được viết tắt là: m(α) + n(β) = 0.
Ta thấy phương trình của chùm mặt phẳng rất đơn giản nhưng nó lại giúp chúng ta giải được rất nhiều bài toán về phương trình mặt phẳng một cách độc đáo và cực kì ngắn gọn.
Ví dụ. Trong không gian Oxyz cho hai mặt phẳng (α) và (β) lần lượt có phương trình
(α) : x + y + 5z – 1 = 0
(β) : 2x + 3y – z + 2 = 0
a) Chứng minh rằng (α) cắt (β) theo giao tuyến Δ.
b) Viết phương trình mặt phẳng (γ) chứa giao tuyến Δ và điểm M(3 ; 2 ;1).
Giải
a) Mặt phẳng (α) và (β) lần lượt có các vecto pháp tuyến:
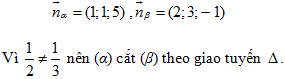
b) Phương trình mặt phẳng (γ) của chùm((α), (β)) có dạng:
m(x + y + 5z – 1) + n(2x + 3y – z + 2) = 0 (1)
Điểm M(3 ; 2 ; 1) thuộc mặt phẳng (γ) nên khi thay toạ độ của M vào (1) ta sẽ tính được các giá trị cụ thể của cặp số (m ; n) để xác định phương trình của (γ).
Ta có : m(x + y + 5z – 1) + n(2x + 3y – z + 2) = 0 ⇔ 9m + 13n = 0.
Chọn m = -13 ta thu được n = 9.
Thay m = -13 và n = 9 vào (1) ta được phương trình của mặt phẳng (γ) cần tìm : 5x + 14y – 74z + 31 = 0.
